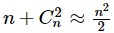神经网络,在近年来的风头正热,我们也来学习一下。
为什么要神经网络
面对高维特征时的线性回归
我们回归一下之前提到的线性回归。
那时候简单起见,我们只说了一元一次线性回归,就是我们只观察一个变量对预测量的影响。
当时的例子中变量为房屋大小,预测量是房屋价格。但是,我们大家都知道,房屋价格肯定不止受房屋大小这一个因素的影响。 比如还有屋子数量、屋子朝向、地理位置、城市名称等。
如果用公式表达就是多元一次方程,如下:
y = m0 + m1 * x1 + m2 *x2 ... m_n * x_n
这时候的我们需要求解的参数(也就是m们)数量是 n + 1 (n是自变量数目),时间复杂度是O(N)。
如果我们觉得一次方程表达力不够,想用二次方程:
y = m_0 + m_1 * x_1 + m_2 * x_2 + m_1_2 * x_1 * x_2 + m_1_1 * x_1^2 + m_2_2 * x_2^2 + .... + m_n_n * x_n^2
这时候参数数量是多少呢? 是:
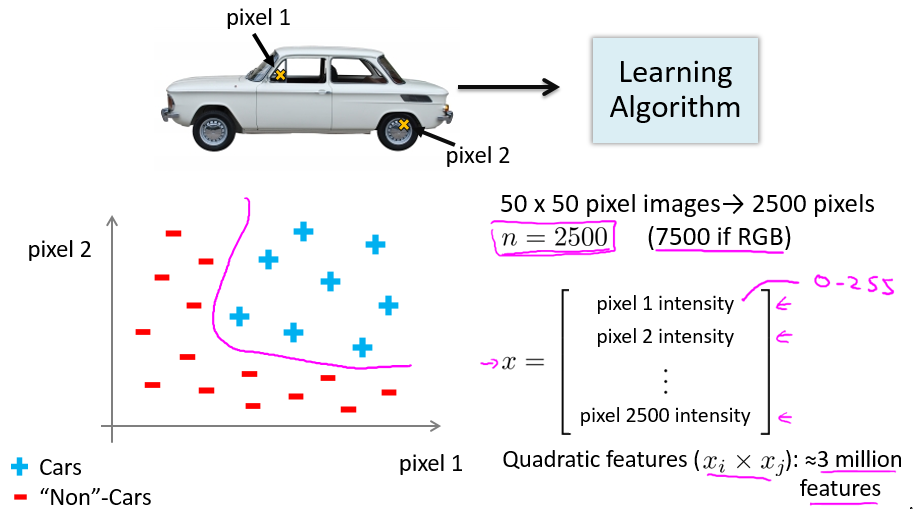
如果房屋的特征由原来的 2 维增加到了 100 维,进行二次多项式扩展后,特征个数达到了约 5000 维,对计算机的性能提出了很大的挑战。
图片数据
在计算机视觉(CV)领域,图像的特征往往都是高维的。
下图中,我们想要区分一幅图像是否是汽车图像,假定图像分辨率为 50×50 ,且每个像素的灰度都为一个特征,那么一副图像的特征维度就高达 2500 维, 进行二次多项式扩展后,特征维度更是达到了约 3000000:
因此,就需要考虑用新的机器学习模型来处理高维特征的非线性分类问题,神经网络是典型的不需要增加特征数目就能完成非线性分类问题的模型。
神经网络定义
人体神经元模型
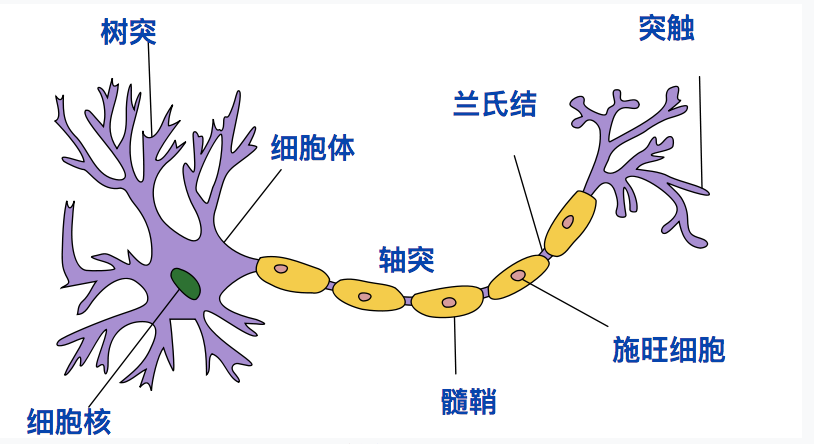
神经网络模型是模仿人类的大脑神经构造而构造的。先来看人体神经元模型。
神经元的可以分为四个区域:
- 接收区(receptive zone):树突接收到输入信息。
- 触发区(trigger zone):位于轴突和细胞体交接的地方,决定是否产生神经冲动。
- 传导区(conducting zone):由轴突进行神经冲动的传递。
- 输出区(output zone):神经冲动的目的就是要让神经末梢,突触的神经递质或电力释出,才能影响下一个接受的细胞(神经元、肌肉细胞或是腺体细胞),此称为突触传递。
人工神经网络
维基百科:
人工神经网络(ANN:Artificial Neural Network),简称神经网络(NN:Neural Network)。迄今为止,人工神经网络尚无统一定义, 其实一种模拟了人体神经元构成的数学模型,依靠系统的复杂程度,通过调整内部大量节点之间相互连接的关系,从而达到处理信息的目的。
上图显示了人工神经网络是一个分层模型,逻辑上可以分为三层:
- 输入层:输入层接收特征向量 x 。
- 输出层:输出层产出最终的预测 h 。
- 隐含层:隐含层介于输入层与输出层之间,之所以称之为隐含层,是因为当中产生的值并不像输入层使用的样本矩阵 X 或者输出层用到的标签矩阵 y 那样直接可见。
前向传播与反向传播
在上面,我们看到了人工神经网络的模型,知道了它分为三层,对于我们来讲,求解神经网络的过程,就是寻找隐含层各个参数的过程。
通常求解有两种方法,分别为前向传播与反向传播。
提前准备
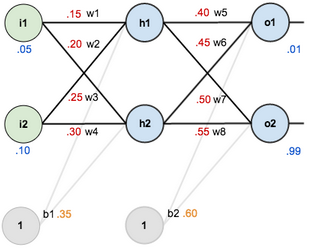
假设神经网络结构如下图所示:有2个输入单元;隐含层为2个神经元;输出层也是2个神经元,隐含层和输出层各有1个偏置。
为了直观,这里初始化权重和偏置量,得到如下效果:
前向传播
前向传播的思想比较简单,就是带上所有变量,一层层地往下算。
隐含层神经元h1的输入,也就是所有指向 h1 的箭头总和:
net_h1 = w_1 * i_1 + w_2 * i_2 + b1 * 1
代入数据:
net_h1 = 0.15 * 0.05 + 0.2 * 0.1 + 0.35 * 1 = 0.3775
这里假设激励函数用logistic函数(也就是在逻辑回归中的那个sigmoid函数),计算得隐含层神经元h1的输出:
同样的方法,可以得到隐含层神经元h2的输出为:
net_h2 = 0.596884378
对输出层神经元重复这个过程,使用隐藏层神经元的输出作为输入。这样输出层神经元O1的输入为:
net_O1 = w_5 * out_h1 + w_6 * out_h2 + b2 * 1
代入数据:
net_O1 = 1.105905967
输出层神经元O1的输出,经由sigmoid函数转换为:
out_O1 = 0.75136507
同样的方法,可以得到输出层神经元O2的输出为:
out_O2 = 0.772928465
统计误差
假如误差公式为:
如上图,O1的原始输出为0.01,而神经网络的输出为0.75136507,则其误差为:
E_O1 = 0.298371109
同理可得,O2的误差为:
E_O2 = 0.023560026
这样,总的误差为:
E_total = E_O1 + E_O2 = 0.2983711109
反向传播
通过前向传播,我们定义了误差,那么如何该调整 w 们,来减少误差 E 呢?这就要反向传播来了。
回顾线性回归我们求解最优解地时候,借助了一个算法,叫做梯度下降算法,从数学角度描述就是求偏导。
如下面这个公式:
它表示了对于 w_5 这个参数对于最终误差的影响。
反向传播的思想总体来讲,就是相当于重新训练了一个神经网络,只不过它的训练方向是从右到左,而前向传播的训练反向是从左到右。
反向传播依托的基石就是数学求偏导的一个特性,叫做 chain rule。正因为借助了chain rule,反向传播才得以实现。