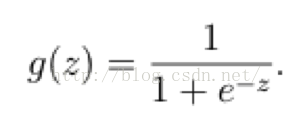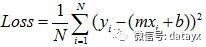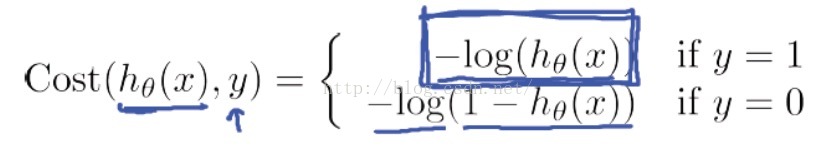上一个篇本系列文章,讲到了线性回归,这次来看看逻辑回归。
出现的背景
回顾线性回归
logistic 回归其实是一种广义线性回归(generalized linear model),那它和我们之前提到的线性回归又什么不同呢?。
之前系列中提到的线性回归,目的是更好地拟合数据,让我们获得更好的函数,来缩小预测值与实际值之间的误差。
线性回归能对连续值结果进行预测,而现实生活中常见的另外一类问题是,分类问题。
最简单的情况是是与否的二分类问题。 比如说医生需要判断病人是否生病,银行要判断一个人的信用程度是否达到可以给他发信用卡的程度,邮件收件箱要自动对邮件分类为正常邮件和垃圾邮件等等。
如果用线性回归怎么做分类呢?简单来想,就是找个阈值,阈值的上下各分为两类。
线性回归的局限性
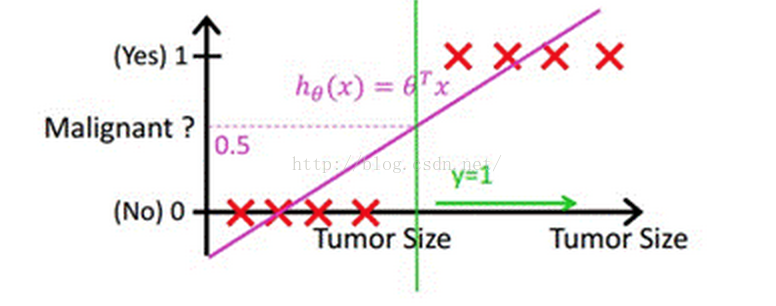
借助Andrew Ng老师的课件中的例子,如下图,下图中X为数据点肿瘤的大小,Y为观测结果是否是恶性肿瘤。通过构建线性回归模型,如hθ(x)所示,构建线性回归模型后,我们设定一个阈值0.5,预测hθ(x)≥0.5的这些点为恶性肿瘤,而hθ(x)<0.5为良性肿瘤。
但很多实际的情况下,我们需要学习的分类数据并没有这么精准,比如说上述例子中突然有一个不按套路出牌的数据点出现,如下图所示:
你看,现在你再设定0.5,这个判定阈值就失效了,而现实生活的分类问题的数据,会比例子中这个更为复杂,而这个时候我们借助于线性回归+阈值的方式,已经很难完成一个鲁棒性很好的分类器了。
逻辑回归的诞生
面对上面的场景,它提出了新的思路:
如果线性回归的结果输出是一个连续值,而值的范围是无法限定的,那我们有没有办法把这个结果值映射为可以帮助我们判断的结果呢。
而如果输出结果是 (0,1) 的一个概率值,这个问题就很清楚了。在数学上还真就有这样一个简单的函数,就是很神奇的sigmoid函数(如下):
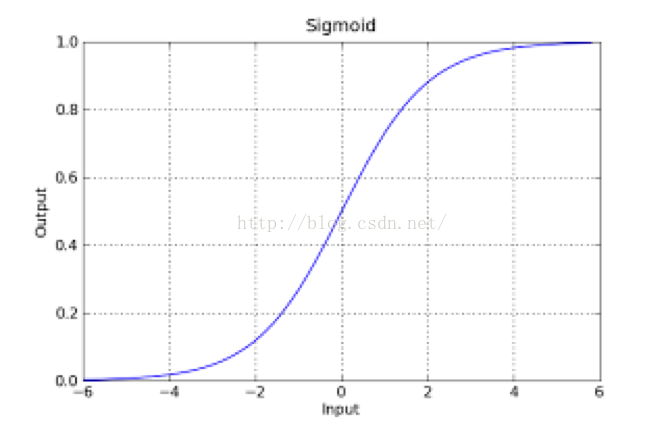
如果把sigmoid函数图像画出来,是如下的样子:
从函数图上可以看出,函数y=g(z)在z=0的时候取值为1/2,而随着z逐渐变小,函数值趋于0,z逐渐变大的同时函数值逐渐趋于1,而这正是一个概率的范围。
所以我们定义线性回归的预测函数为 Y = W^T * X,那么逻辑回归的输出 Y = g(W^T * X),其中y=g(z)函数正是上述sigmoid函数(或者简单叫做S形函数)。
几个概念
判定边界
判定边界,可以理解为是用以对不同类别的数据分割的边界,边界的两旁应该是不同类别的数据。
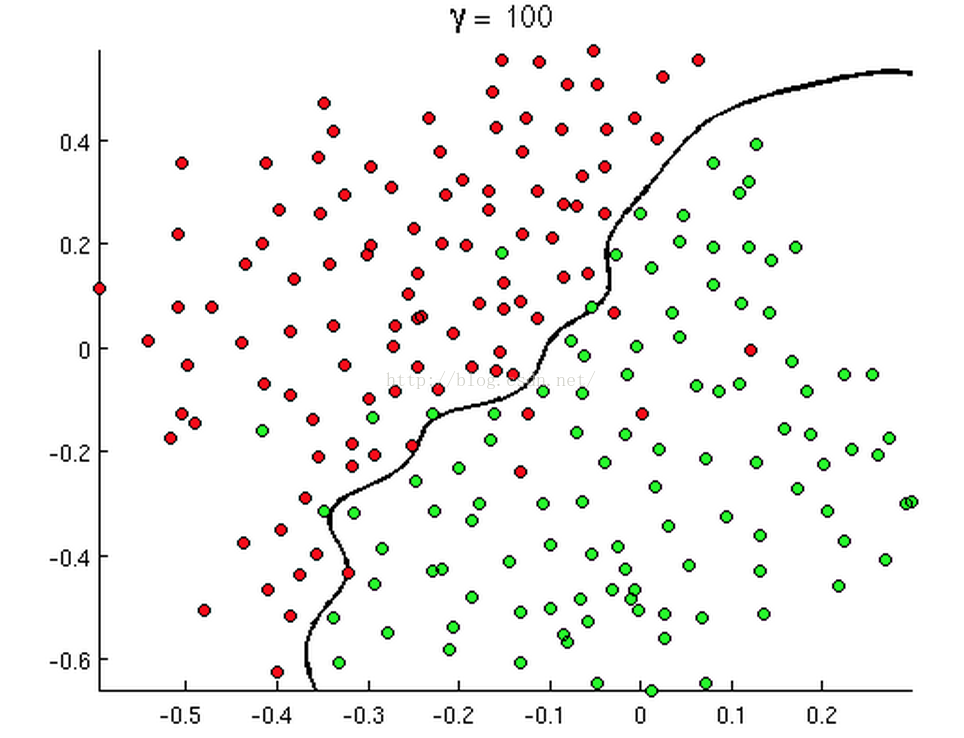
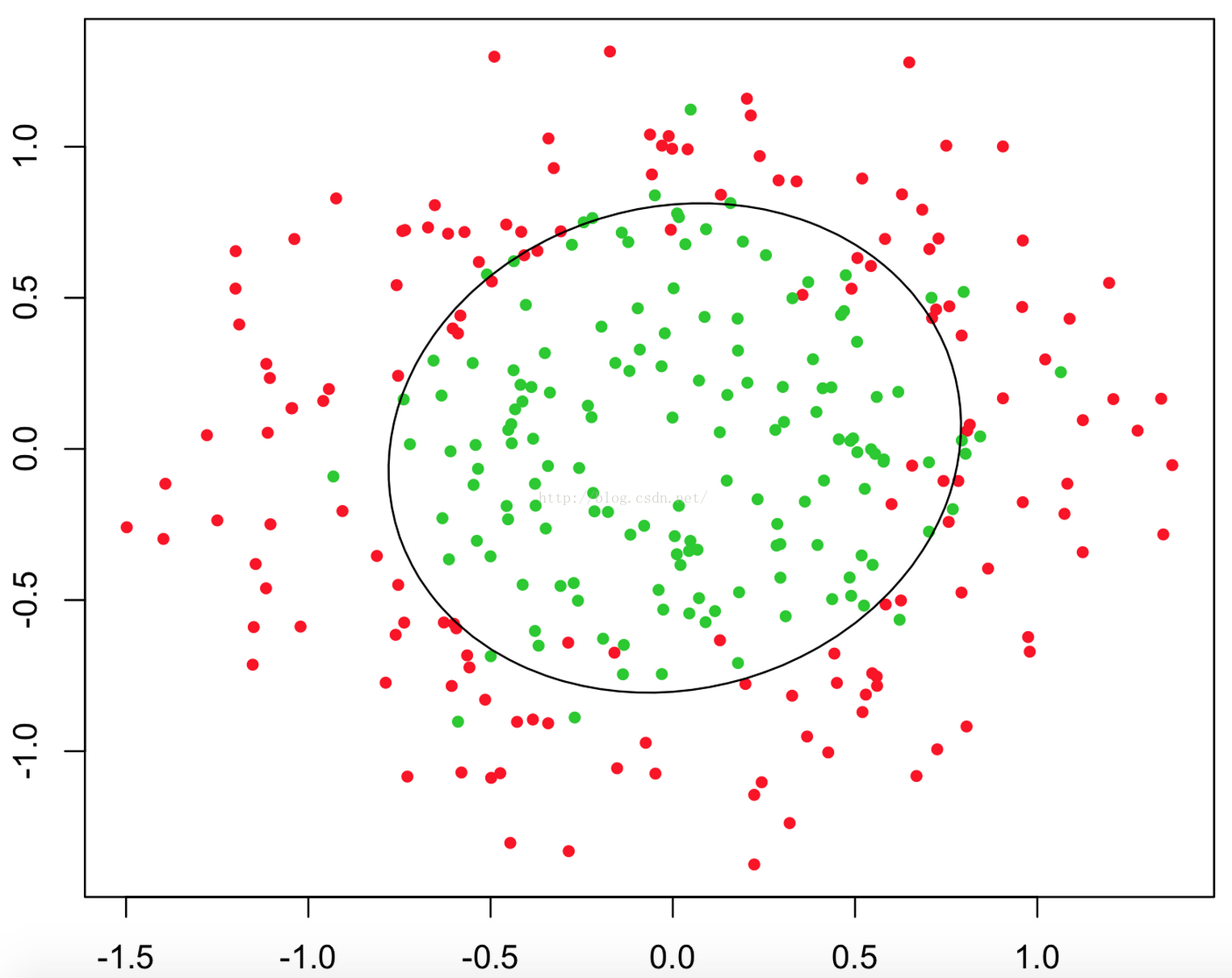
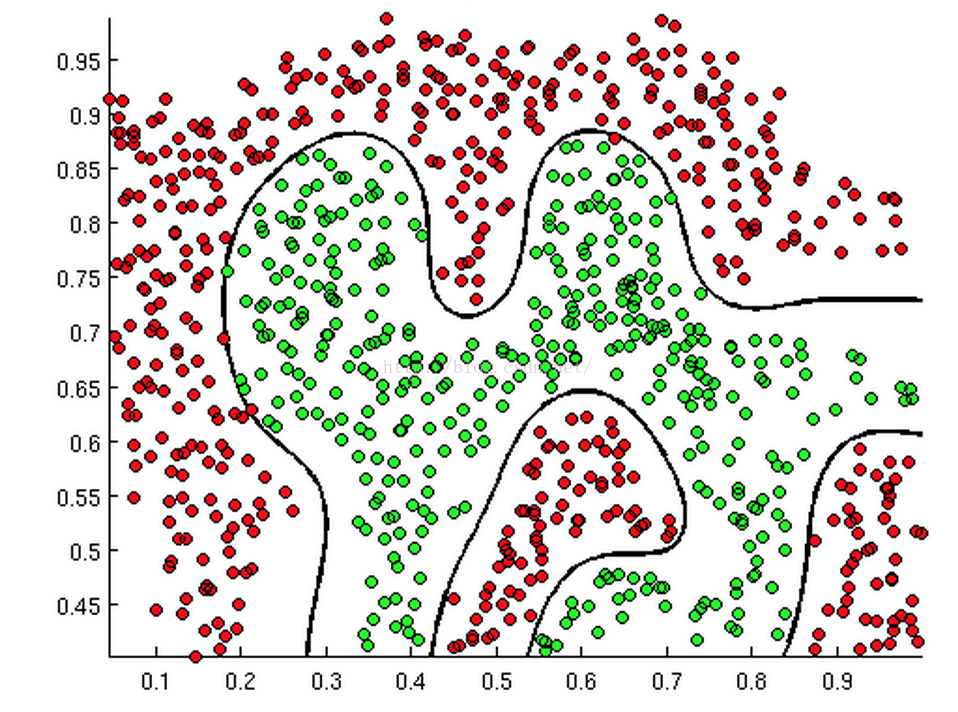
如下面几张图:
上述三张图中的直线、圆和曲线就是所谓的判断边界,它能将两类样本分割开来。
如何获取判定边界
以下的解释会有些数学性,不要慌,慢慢看。
- 我们定义了逻辑回归的函数为:Y = g(W^T * X),其中的 g 函数就是 sigmoid 函数。
- 那么当 g(W^T * X) >= 0.5,根据 g 函数,也就是sigmoid 函数的特性,此时我们可以得到 W^T * X >= 0,以及 Y = 1。 (换句话说就是,当概率大于等于0.5时,我们认为结果 Y 是正样本,而且g函数的输入必然是大于等于0)
- 反之,当 g(W^T * X) < 0.5,我们可以得到 W^T * X < 0,以及 Y = 0。
有没有发现,预测结果是0还是1,都是取决于 W^T * X 是否大于等于 0。 所以, W^T * X = 0 就是我们要找的判定边界。
回到上面的三幅图中的判断边界,不管它是直线、圆和曲线,只要我们能够找到足够好的 W^T * X 来描述它,我们就可以对数据进行分类。
代价函数
代价函数(cost function),就是一种衡量我们在这组参数下预估的结果和实际结果差距的函数。
回想线性回归,那个定义误差大小的函数,其实就是代价函数:
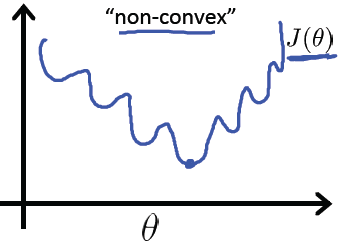
但是对于逻辑回归,如果我们直接把 Y 替换为现在的 g(W^T * X) , 得出的函数时“非凸”的,如下图:
上面的函数有很多的局部最小点,不利于我们寻找全局最小点。
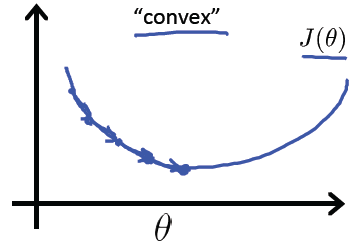
我们希望代价函数是像个碗一样的,它只有一个最低点,既是局部最小点,也是全局最小点。如下图:
经过大量的前辈努力,我们找到了这个代价函数的定义方式:
训练
定义好代价函数后,就可以继续下一步了,就是找到最低点。
这一步可以参考线性回归里提到的梯度下降算法。
动手练习
已经有前辈实现过了,代码可以在 GitHub 上查看:地址.