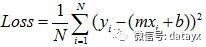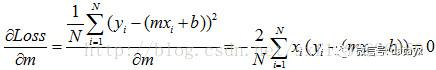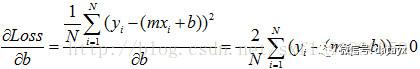线性回归是机器学习中最基本的一个算法。但它“麻雀虽小,五脏俱全”,仔细理解后,将有助于我们更加了解机器学习。
什么是线性回归
线性回归是监督学习中的一种。 如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。
线性回归分为一元线性回归和多元线性回归。
一元的是只有一个x和一个y。 也就是以前数学里常见的:
y = mx + b;
m 和 b 是参数。
多元的是指有多个x和一个y。
y = a1 * x^1 + a2 * x^2 + a3 * x^3 + ... + b
我们这次只看一元线性回归。
提前准备
为了便于理解,我们以预测房价为实际例子。
房价的高低,可变因素很多。但简单起见,我们知道房子越大,总价应该是越高的。所以这次我们只关系一个变量:房屋大小。
比如数据可以是这个样子的(我自己随便造的):
| area | prices |
|---|---|
| 100 | 100 |
| 200 | 130 |
| 300 | 170 |
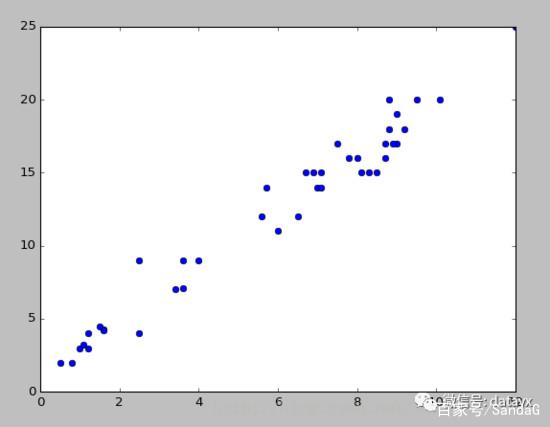
如何在一个二维坐标系上表示这些数据呢? 自变量定为 area,也就是 x 坐标,因变量定位 prices, 也就是 y 左边。
来把这些点画到坐标系上看一看。
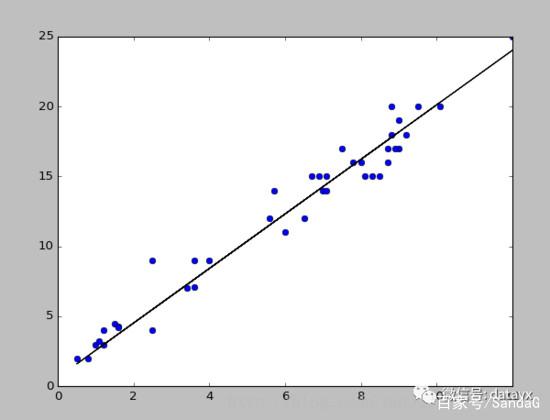
对于一元线性回归来讲,我们希望找到一个 m 和 b, 可以满足输入任意的 x ,我们都能得到一个 y, 这个 y 就是我们对于结果的预测。
在坐标系上表示,就是来找一条直线,这条直线能以最小的误差(Loss)来拟合数据。如下:
定义误差
寻找最小误差的第一步,就是定义误差。
对于二维坐标系上的任意一点(x_i, y_i)来说,它到直线 y = m * x + b 的纵坐标距离为:
| y_i - (m * x_i + b) |
简单起见,将绝对值变为平方。那么把平面上所有点离直线的距离加起来,就是得到了我们想要的误差。
一般我们还会把Loss求和平均,来当作最终的损失。
而我们的目标就是找到合适的 m 和 b,使得这个函数值的最小。
怎么找最小误差
一般有两个方法:最小二乘法和梯度下降法。
最小二乘法
对于上面的 Loss 方程,x、y、i、N 都是已知的,那么我们就可以把这个方程看作是m和b的方程。
作为一个m和b的二次方程,那么求 Loss 最小值的问题就转变成了求极值问题,这个高数学过的都应该知道点。
求极值的方法,就是当初高数学的,令每个变量的偏导数为零,求方程组的解即可。
然后把 m 和 b 求出来,就可以了。
梯度下降法
梯度下降法的基本思想可以类比为一个寻找谷底的过程。如下图:
在山上寻找谷底,要确定三个条件。 首先是方向(也就是梯度),其次是步子大小(步长),最后是走多少步(迭代次数)。
梯度下降法的缺点是到最小点的时候收敛速度变慢,并且对初始点的选择极为敏感,其改进大多是在这两方面下功夫。
最小二乘法与梯度下降法比较
相同点
-
本质相同:
两种方法都是在给定已知数据(independent & dependent variables)的前提下对dependent variables算出出一个一般性的估值函数。 然后对给定新数据的dependent variables进行估算。
-
目标相同:
都是在已知数据的框架内,使得估算值与实际值的总平方差尽量更小。
不同点
-
实现方法和结果不同:
最小二乘法是直接对 Loss 求导找出全局最小,是非迭代法。 而梯度下降法是一种迭代法,先给定一个点 (m, b),然后向 Loss 下降最快的方向调整,在若干次迭代之后找到局部最小。
实例分析:波士顿房价
导入数据
从Scikit-learn的数据集里载入波士顿的房价数据:
from sklearn import datasets
boston = datasetd.load_boston()
我们可以打印其描述文档来获取其各项属性:
print boston.DESCR
分割训练集、测试集
我们先给定一个默认的采样频率,如0.5,用于将训练集和测试集分为两个相等的集合:
sampleRatio = 0.5
n_samples = len(boston.target)
sampleBoundary = int(n_samples * sampleRatio)
接着,洗乱整个集合,并取出相应的训练集和测试集数据:
shuffleIdx = range(n_samples)
numpy.random.shuffle(shuffleIdx) # 需要导入numpy
# 训练集的特征和回归值
train_features = boston.data[shuffleIdx[:sampleBoundary]]
train_targets = boston.target[shuffleIdx[:sampleBoundary]]
# 测试集的特征和回归值
test_features = boston.data[shuffleIdx[sampleBoundary:]]
test_targets = boston.target[shuffleIdx[sampleBoundary:]]
接下来,获取回归模型,拟合并得到测试集的预测结果:
lr = sklearn.linear_model.LinearRegression() # 需要导入sklearn的linear_model
lr.fit(train_features, train_targets) # 拟合
y = lr.predict(test_features) # 预测
最后,把预测结果通过matplotlib画出来:
import matplotlib.pyplot as plt
plt.plot(y, test_targets, 'rx') # y = ωX
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'b-.', lw=4) # f(x)=x
plt.ylabel("Predieted Price")
plt.xlabel("Real Price")
plt.show()
得到的结果如下: