定义
K最近邻(kNN,k-Nearest Neighbor)分类算法是数据挖掘分类技术中最简单的方法之一。
kNN算法是监督学习中分类方法的一种。
所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用它最接近的k个邻居来代表。
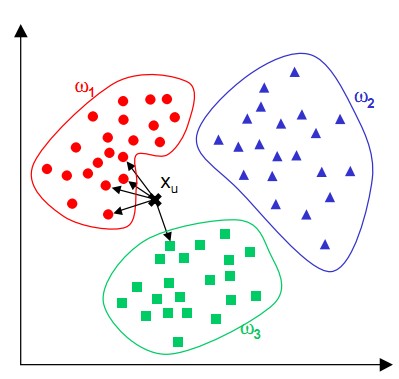
kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。用句俗话来说,就是“近朱者赤,近墨者黑”。
KNN算法不仅可以用于分类,还可以用于回归。通过找出一个样本的k个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight),如权值与距离成反比。
算法步骤
-
准备数据,对数据进行预处理
-
选用合适的数据结构存储训练数据和测试元组
- 设定参数,如 k
- 维护一个大小为k的的按距离由大到小的优先级队列,用于存储最近邻训练元组。随机从训练元组中选取k个元组作为初始的最近邻元组,分别计算测试元组到这k个元组的距离,将训练元组标号和距离存入优先级队列
- 遍历训练元组集,计算当前训练元组与测试元组的距离,将所得距离L 与优先级队列中的最大距离Lmax
-
进行比较。若 L >=Lmax,则舍弃该元组,遍历下一个元组。若L < Lmax,删除优先级队列中最大距离的元组,将当前训练元组存入优先级队列。
-
遍历完毕,计算优先级队列中k 个元组的多数类,并将其作为测试元组的类别。
- 测试元组集测试完毕后计算误差率,继续设定不同的k值重新进行训练,最后取误差率最小的k 值。
在KNN中,通过计算对象间距离来作为各个对象之间的非相似性指标,避免了对象之间的匹配问题,在这里距离一般使用欧氏距离或曼哈顿距离:
存在的问题
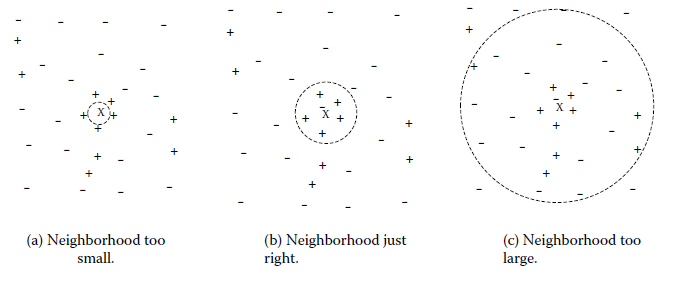
k值得选取对kNN学习模型有着很大的影响。若k值过小,预测结果会对噪音样本点显得异常敏感。特别地,当k等于1时,kNN退化成最近邻算法,没有了显式的学习过程。若k值过大,会有较大的邻域训练样本进行预测,可以减小噪音样本点的减少;但是距离较远的训练样本点对预测结果会有贡献,以至于造成预测结果错误。下图给出k值的选取对于预测结果的影响:
优缺点
优点
-
简单,易于理解,易于实现,无需估计参数,无需训练;
- 适合对稀有事件进行分类;
- 特别适合于多分类问题(multi-modal,对象具有多个类别标签), kNN比SVM的表现要好
缺点
该算法在分类时有个主要的不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。 该算法只计算“最近的”邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。无论怎样,数量并不能影响运行结果。
该方法的另一个不足之处是计算量较大,因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。
可理解性差,无法给出像决策树那样的规则。
参考
- https://baike.baidu.com/item/%E9%82%BB%E8%BF%91%E7%AE%97%E6%B3%95/1151153
- http://www.cnblogs.com/en-heng/p/5000628.html